Vector Similarity Search
벡터 유사도 검색(Vector Similarity Search)은 데이터를 숫자의 배열인 벡터로 표현하고, 이 벡터들 간의 유사도를 측정하여 가장 유사한 데이터를 찾아내는 방법입니다. 예를 들어, ‘Cat’이라는 단어는 ‘Dog’와 ‘Kitten’ 중에서 ‘Kitten’과 더 비슷한 맥락에서 사용될 것입니다. 또 다른 예시로, ‘Dog’와 ‘Wolf’ 중에서는 ‘Dog’의 쓰임새가 ‘Cat’과 더 유사하다고 볼 수 있습니다.
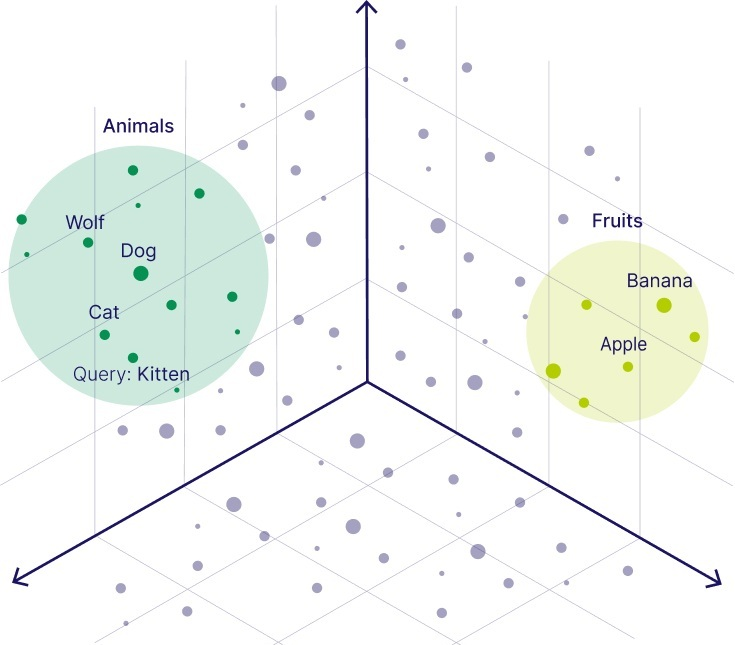
그림 1. Word Embeddings
© Weaviate
여기서 ‘쓰임새가 유사하다’는 것은 단어의 의미 정보(semantic)가 유사하다고 볼 수 있습니다. 이러한 의미 정보를 벡터로 표현하는 것을 임베딩(Embedding)이라고 하며, 임베딩 모델은 의미가 유사할수록 벡터 간의 거리가 가깝게 표현되도록 지도 학습을 받습니다. 임베딩은 단어뿐만 아니라 문장 단위에서도 동일하게 적용될 수 있으며, 임베딩과 벡터 유사도 검색을 통해 RAG(Retrieval-Augmented Generation)에서 문서를 효과적으로 검색할 수 있게 됩니다.
kNN (k-Nearest Neighbors)
벡터 유사도 검색을 위해서는 기본적으로 벡터들의 유사도를 측정하기 위한 알고리즘이 필요합니다. 이 때 사용하는 것이 kNN(k-최근접 이웃)입니다. kNN 알고리즘은 유사한 데이터의 벡터는 특징 공간(feature space)에서 서로 가까이 위치한다는 가정을 이용해서 벡터 포인트 간의 거리를 계산하고 분류하는 머신러닝 알고리즘입니다.
kNN 알고리즘의 가장 기본적인 형태는 Brute Force 방법을 이용해서 모든 포인트 간의 거리를 직접 계산하는 것 입니다. 하지만 이러한 방식은 차원이 커지고, 데이터가 많아질수록 모든 포인트와의 거리를 계산해야하기 때문에 굉장히 느려질 수 밖에 없습니다. 그래서 실제 상황에서는 모든 포인트와의 거리를 구하지 않고 일부 포인트와의 거리만을 계산하는 근사적인 최근접 이웃(Approximate K-Nearest Neighbor) 알고리즘을 사용합니다.
HNSW (Hierarchical Navigable Small World)
HNSW는 AkNN(Approximate K-Nearest Neighbor) 알고리즘의 한 종류로 이는 가장 가까운 이웃을 ‘근사적으로’ 찾는 방식이기 때문에 전역 최적해(global minima)를 보장하지는 않습니다.
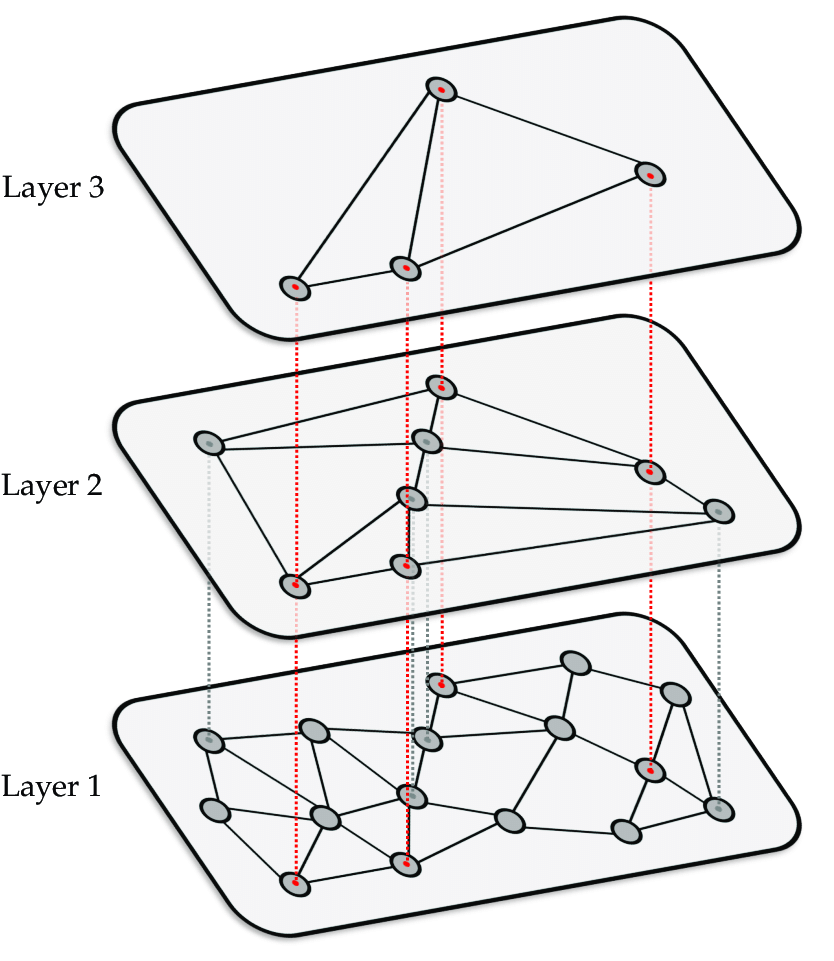
그림 2. Illustration of HNSW graph
Frank Zalkow, Julian Brandner, Meinard Müller (2021)
HNSW의 검색 원리
우리가 가진 모든 벡터 데이터를 Figure 2의 Layer 1처럼 그래프의 노드로 표현했다고 가정해 봅시다. 이때 각 노드는 항상 가장 가까운 노드와 우선적으로 연결됩니다.
만약 이러한 그래프가 있다면, 쿼리가 입력되었을 때 탐색의 시작점이 어떤 노드인지에 따라 탐색 속도가 크게 달라질 수 있습니다. 탐색 시작점이 실제 쿼리와 가까운 위치였다면 탐색이 빠르게 끝나겠지만, 거리가 먼 곳에서 시작했다면 최근접 노드를 찾기 위해 많은 탐색 시간이 필요할 것입니다. 그렇기 때문에 최적의 진입점(entry point)을 찾는 것은 그래프 기반 최근접 이웃 탐색에서 매우 중요합니다.
이러한 최적의 진입점을 찾기 위해 HNSW가 택한 방법은 계층 구조입니다. 그림에서 상위 레이어(Layer 2)는 하위 레이어(Layer 1)의 진입점을 찾기 위해 존재합니다. 상위 레이어는 하위 레이어의 일부 노드만을 복제하여 보유합니다. 따라서 상위 레이어에서는 무작위 진입점을 가지고 시작해도 하위 레이어보다 더 적은 시간을 소모하여 최근접 이웃을 찾을 수 있습니다. 이렇게 찾은 상위 레이어의 최근접 이웃은 하위 레이어의 진입점이 됩니다. 이러한 계층 구조 메커니즘을 통해 HNSW는 모든 노드를 탐색하지 않아도 근사 최적해를 보장할 수 있습니다.
HNSW의 주요 하이퍼파라미터
M : Max Connection
각 노드가 HNSW 그래프의 각 레이어에서 가질 수 있는 최대 양방향 연결(엣지)의 수
efConstruction
HNSW 인덱스를 구축하거나 새로운 노드를 삽입할 때, 각 노드가 자신의 이웃을 찾기 위해 탐색하는 후보 이웃 노드의 최대 수. (이 값은 얼마나 "꼼꼼하게" 주변을 탐색하여 최적의 연결을 만들지를 결정합니다.)
ef : efSearch
실제 쿼리의 최근접 이웃을 탐색할 때, 현재까지 찾은 최적의 후보 노드 목록(dynamic candidate list)의 최대 크기
- 높은
ef: 검색 정확도(Recall) 향상, 검색 시간(Latency) 증가 - 낮은
ef: 검색 정확도 저하, 검색 시간 단축
mL : Level Multiplier
각 노드가 더 높은 레이어에 포함될 확률, 일반적으로 $1/ln(M)$ 값을 사용
- 너무 높은
mL: 상위 레이어 노드의 수 증가. 계층 탐색의 이점 감소. 탐색 시간을 증가 - 너무 낮은
mL: 상위 레이어 노드의 수 감소. 최적의 진입점을 찾기 불가능. 탐색 시간을 증가
요약하자면, M과 efConstruction에 따라 최하위 레이어에서 그래프가 생성되고, mL에 의해 선별된 노드들은 상위 레이어로 올라가 동일한 과정을 반복합니다. 이렇게 만들어진 계층적 그래프를 통해 효율적으로 벡터를 탐색하게 되는 것입니다.
HNSW에 대한 TMI
HNSW에는 한 가지 까다로운 문제점이 존재합니다. 삽입(insert)은 비교적 간단하지만, 삭제(delete)의 경우 기존 방법론들과 달리 큰 문제가 될 수 있기 때문입니다. 만약 노드가 제거될 때 연결을 재정의하지 않으면 특정 노드는 의도치 않게 모든 연결이 끊기는 등의 그래프의 무결성이 손상될 수 있기 때문입니다.
이러한 문제를 해결하기 위해 HNSW에서는 일반적으로 그래프에서 노드를 즉시 제거하기보다는 비활성화하는 방식을 채택하고 있습니다. 삭제된 노드들을 “삭제된 노드”로 표시한 후 커넥션은 유지합니다. 그리고 일정 주기마다 정리(vacuuming)하거나 재구성(rebalancing)하는 lazy deletion 방식을 사용합니다.
HNSW는 초기에 그래프를 구축하는 데 비교적 많은 비용이 들지만, 검색 속도와 정확도 면에서는 높은 성능을 보장합니다. 그렇기 때문에 HNSW는 현존하는 AkNN 방법론 중 가장 효율적이고 널리 사용되는 알고리즘 중 하나입니다. 물론 같은 HNSW라도 메모리 최적화 방법이나, 다양한 트레이드오프를 통해 개선된 버전들이 계속 연구되고 있습니다.
Vector Similarity
kNN 알고리즘에서 벡터 간의 거리를 계산할 때, 기본적으로 Euclidean(L2) 거리를 생각할 수 있습니다. 이는 벡터 간의 물리적인 ‘거리’를 기반으로 유사도를 측정하는 방식입니다. 하지만 이러한 방식에는 몇 가지 문제점이 있습니다.
거리 기반 유사도의 경우 낮은 차원에서는 충분히 효과적으로 포인트 간을 구분하는 변별력을 가지고 있지만, 차원이 커지면 커질수록 모든 데이터 포인트 간의 거리가 비슷하게 멀어지는 현상이 발생합니다. 이를 차원의 저주(Curse of Dimensionality)라고 부릅니다.
차원의 저주란 쉽게 말해서 3가지 정도의 특징(키, 취미, 좋아하는 색 등)을 놓고 봤을 때는 나와 전혀 다르거나 굉장히 유사한 사람을 찾을 수 있겠지만, 10,000가지 특징(키, 취미, 습관, 좋아하는 색, 좋아하는 동물, 신발 끈 묶는 방식, 어릴 적 기억, 숨 쉬는 방식 등)을 놓고 비교하면 대부분의 사람들이 너무 많이 다르기 때문에 사실상 누가 더 비슷하거나 다른지 구분하는 것 자체가 무의미할 정도로 서로 너무 다르다고 느끼게 됩니다. 이러한 문제점을 보안하기 위해서 고 차원 벡터의 경우, 각도 기반 유사도를 채택하기도 합니다.
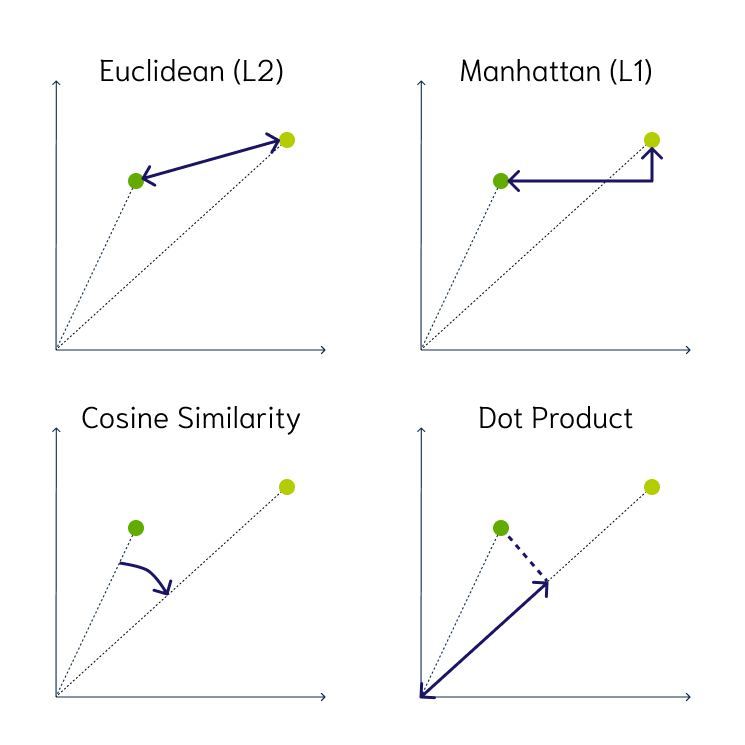
그림 3. Vector Similarity
© Weaviate
각도 기반 유사도라고 해서 차원의 저주에서 완전히 자유로운 것은 아닙니다. 하지만 정규화 과정을 한 번 거치기 때문에 각 특성(feature)이 미치는 영향력을 균일하게 만들어서 주어 비교적 높은 차원에서도 변별력을 잃지 않는 모습을 보여줍니다.
| Distance-based | Angle-based |
|---|---|
| 직관적 | 비직관적 |
| 크기 정보 유지 | 크기 정보 손실 |
| 정규화하기 어려움 | 정규화된 데이터 |
| 고차원에서 변별력 상실 | 차원에 저주에 덜 민감 |
결론
벡터 유사도 검색이란 RAG에서 저장된 데이터 중에 입력 데이터와 높은 연관성을 보이는 데이터를 검색하기 위해서 데이터를 벡터화(임베딩)하고 벡터 간의 유사도를 측정하여 원하는 결과를 얻는 과정을 말합니다.
최근에는 HNSW 같은 AkNN 알고리즘을 사용하여, 유사한 데이터를 탐색하며, 기존에도 지도 학습 머신 러닝 방법론으로 자주 사용되었지만 최근들어 RAG와 연계되어 많은 파생 알고리즘과 라이브러리 등이 개발되고 있습니다. RAG를 사용하기 위해서 반드시 알아야하는 내용은 아니지만, 기본적인 배경지식은 가지고 있다면 반드시 도움이 될 것이라 생각됩니다.
Reference
[1] Monigatti, Leonie (2023) | A Gentle Introduction to Vector Databases
[2] Zalkow, Frank (2020) | Efficient Retrieval of Music Recordings Using Graph-Based Index Structures
